
题目列表(包括答案和解析)
如图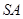 ⊥平面
⊥平面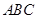 ,
,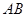 ⊥
⊥ ,过
,过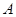 做
做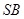
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
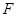 ,求证
,求证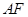 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
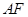 ⊥
⊥
只需证  ⊥平面
⊥平面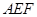
只需证 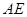 ⊥
⊥ (因为
(因为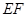 ⊥
⊥ )
)
只需证 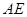 ⊥平面
⊥平面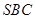
只需证 ① (因为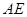 ⊥
⊥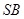 )
)
只需证  ⊥平面
⊥平面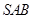
只需证 ② (因为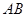 ⊥
⊥ )
)
由只需证 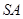 ⊥平面
⊥平面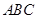 可知上式成立
可知上式成立
所以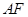 ⊥
⊥
把证明过程补充完整① ②
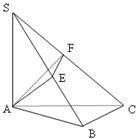
 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
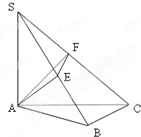
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程: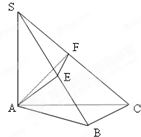 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:请先阅读:
设平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
当且仅当è=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)试求函数![]() 的最大值.
的最大值.
 =(a1,a2),
=(a1,a2),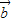 =(b1,b2),且
=(b1,b2),且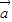 与
与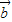 的夹角为θ,
的夹角为θ,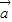 •
•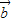 =|
=|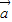 ||
||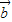 |cosθ,
|cosθ,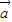 •
•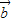 ≤|
≤|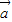 ||
||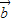 |.
|.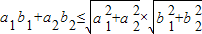 ,
,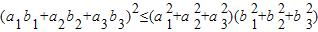 成立;
成立;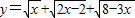 的最大值.
的最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com