
题目列表(包括答案和解析)
(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是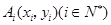 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
(1) 若点 为抛物线
为抛物线
 准线上
准线上
一点,点 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线
 经
经
过该抛物线的焦点,证明 .
.
(2)若点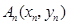 要么落在
要么落在 所表示的曲线上,
所表示的曲线上,
要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,
,
试写出 (不需证明);
(不需证明);
(3)若点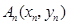 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求 的表达式.
的表达式.

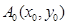 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是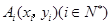 ,(如图所示,
,(如图所示,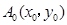 坐标以已知条件为准),
坐标以已知条件为准),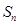 表示青蛙从点
表示青蛙从点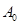 到点
到点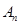 所经过的路程。
所经过的路程。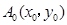 为抛物线
为抛物线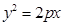
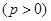 准线上
准线上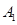 ,
,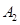 均在该抛物线上,并且直线
均在该抛物线上,并且直线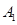
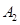 经
经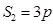 .
.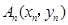 要么落在
要么落在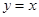 所表示的曲线上,
所表示的曲线上,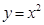 所表示的曲线上,并且
所表示的曲线上,并且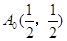 ,
,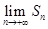 (不需证明);
(不需证明);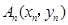 要么落在
要么落在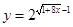 所表示的曲线上,要么落在
所表示的曲线上,要么落在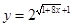 所表示的曲线上,并且
所表示的曲线上,并且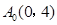 ,求
,求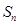 的表达式.
的表达式.
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为![]() 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量![]() (件)与电视广告每天的播放量
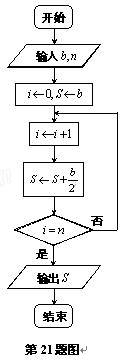
(件)与电视广告每天的播放量![]() (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
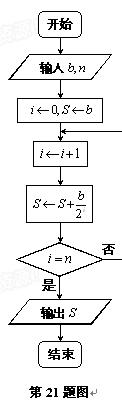
(1)试写出该产品每天的销售量![]() (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量![]() (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加![]() ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式![]() :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点![]() 变换到这一平面上的一点
变换到这一平面上的一点![]() .
.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2) 若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换![]() 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为![]() 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量![]() (件)与电视广告每天的播放量
(件)与电视广告每天的播放量![]() (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
(1)试写出该产品每天的销![]() 售量
售量![]() (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量![]() (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加![]() ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com