
题目列表(包括答案和解析)
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换 :
: 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线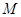 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线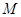 在变换
在变换 下的不动点.
下的不动点.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程. 并求出当
的标准方程. 并求出当 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2)当 时,求(1)中的椭圆
时,求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
 :
: (
( ,
, )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是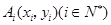 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
(1) 若点 为抛物线
为抛物线
 准线上
准线上
一点,点 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线
 经
经
过该抛物线的焦点,证明 .
.
(2)若点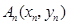 要么落在
要么落在 所表示的曲线上,
所表示的曲线上,
要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,
,
试写出 (不需证明);
(不需证明);
(3)若点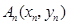 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求 的表达式.
的表达式.

(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
.
(1)若椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标;
(2) 若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换![]() :
:![]() 可把平面直角坐标系上的点
可把平面直角坐标系上的点![]() 变换到这一平面上的点
变换到这一平面上的点![]() .特别地,若曲线
.特别地,若曲线![]() 上一点
上一点![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 与点
与点![]() 重合,则称点
重合,则称点![]() 是曲线
是曲线![]() 在变换
在变换![]() 下的不动点.
下的不动点.
(1)若椭圆![]() 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在![]() 轴上,且焦距为
轴上,且焦距为![]() ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆![]() 的标准方程. 并求出当
的标准方程. 并求出当![]() 时,其两个焦点
时,其两个焦点![]() 、
、![]() 经变换公式
经变换公式![]() 变换后得到的点
变换后得到的点![]() 和
和![]() 的坐标;
的坐标;
(2)当![]() 时,求(1)中的椭圆
时,求(1)中的椭圆![]() 在变换
在变换![]() 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
![]() :
:![]() (
(![]() ,
,![]() )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足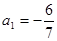 ,
,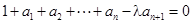 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),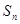 为数列{an}的前
为数列{an}的前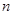 项和.
项和.
(1) 若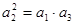 ,求
,求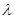 的值;
的值;
(2) 求数列{an}的通项公式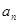 ;
;
(3) 当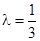 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com