
题目列表(包括答案和解析)
(本小题满分14分)设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(Ⅰ)求![]() 的值,猜想
的值,猜想![]() 的表达式,并用数学归纳法证明;
的表达式,并用数学归纳法证明;
(Ⅱ)将数列![]() 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ,
,![]() );(
);(![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ),(
),(![]() ,
,![]() ,
,![]() ,
,![]() );(
);(![]() ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(本小题满分14分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为 ,求
,求 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
(本小题满分14分)(注意:在试题卷上作答无效)
设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上.
的图象上.
(Ⅰ)求 及数列
及数列 的通项公式
的通项公式 ;
;
(Ⅱ) 将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值;
(Ⅲ)令 (
( ),求证:
),求证:
(本小题满分14分)(注意:在试题卷上作答无效)
设数列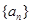 的前
的前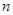 项和为
项和为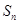 ,对一切
,对一切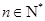 ,点
,点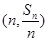 都在函数
都在函数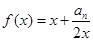 的图象上.
的图象上.
(Ⅰ)求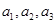 及数列
及数列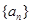 的通项公式
的通项公式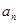 ;
;
(Ⅱ) 将数列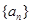 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(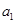 ),(
),( ,
,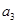 ),(
),(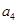 ,
,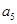 ,
,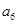 ),(
),(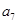 ,
,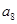 ,
,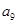 ,
, );(
);(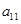 ),(
),(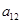 ,
,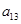 ),(
),(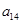 ,
,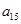 ,
,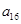 ),(
),(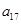 ,
,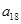 ,
,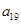 ,
,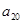 );(
);(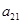 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为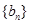 ,求
,求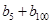 的值;
的值;
(Ⅲ)令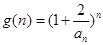 (
( ),求证:
),求证: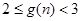
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com