
题目列表(包括答案和解析)
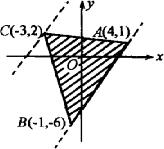
如图所示,设S为平面上以点A(4,1),B(-1,-6),C(-3,2)为顶点的三角形区域(三角形内部及边界),试求当点(x,y)在区域S上变动时t=4x-3y的最大值和最小值.
如图所示的框图是解决某个问题而绘制的流程图,仔细分析各图框内的内容及图框之间的关系,完成下面的问题:

(1)框中x=a的含义是什么?
(2)图框中y=-x2+mx的含义是什么?
(3)该流程图解决的是怎样的一个问题?
(4)当输入的x值为0和4时,输出的值相等,问当输入的x值为3时,输出的值为多大?
(5)要想使输出的值最大,输入的x值应为多少?
(6)按照这个程序框图,当输入的x的值都大于2时,x值大的输出的y值反而小,为什么?
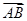 =(6,1),
=(6,1),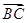 =(x,y),
=(x,y),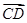 =(-2,-3),若
=(-2,-3),若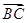 ∥
∥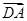 且
且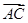 ⊥
⊥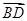 ,则四边形ABCD的面积S为( )
,则四边形ABCD的面积S为( )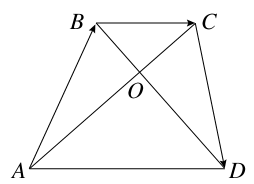
| A.16 | B.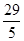 | C. | D. |
如图, =(6,1),
=(6,1),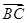 =(x,y),
=(x,y), =(-2,-3),若
=(-2,-3),若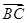 ∥
∥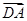 且
且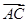 ⊥
⊥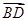 ,则四边形ABCD的面积S为( )
,则四边形ABCD的面积S为( )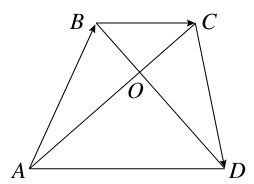
| A.16 | B. | C.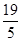 | D.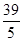 |
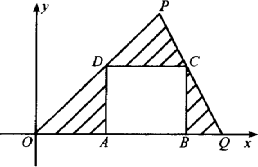
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
(1)问:直线PQ是否能通过下面的点M(6,1),N(4,5);
(2)在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在OP上.
①求证:顶点C一定在直线y=![]() x上;
x上;
②求如图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com