
题目列表(包括答案和解析)
已知函数y=Asin(ωx+Φ)+B(A>0,ω>0,|Φ<![]() |)的周期为T,在一个周期内的图像如图所示,则正确的结论是
|)的周期为T,在一个周期内的图像如图所示,则正确的结论是
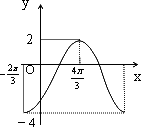
A=3,T=2π
B=-1,ω=2
T=4π,![]() =-
=-![]()
A=3,![]() =
=![]()
如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+![]() )(A>0,ω>0),当x∈[-4,0]时的图像,且图像的最高点为B(-1,2),赛道的中间部分为长
)(A>0,ω>0),当x∈[-4,0]时的图像,且图像的最高点为B(-1,2),赛道的中间部分为长![]() 千米的直线跑道CD,且CD∥EF,赛道的后一部分是以O为圆心的一段圆孤
千米的直线跑道CD,且CD∥EF,赛道的后一部分是以O为圆心的一段圆孤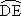 .
.
(1)求ω的值和∠DOE的大小;
(2)若要在圆孤赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆孤 上,且∠POE=
上,且∠POE=![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
如图是函数y=Asin(ωx+φ) 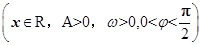 在区间
在区间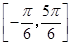 上的图像.为了得到这个函数的图像,只需将y=sin x(x∈R)的图像上所有的点( )
上的图像.为了得到这个函数的图像,只需将y=sin x(x∈R)的图像上所有的点( )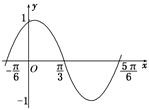
A.向左平移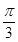 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的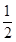 ,纵坐标不变 ,纵坐标不变 |
B.向左平移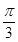 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移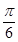 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的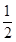 ,纵坐标不变 ,纵坐标不变 |
D.向左平移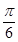 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是水深数据:
据上述数据描成的曲线如图所示,经拟合,该曲线可近似地看成正弦函数y=Asinωx+b的图像.

(1)试根据数据表和曲线,求出y=Asinωx+b的表达式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间(忽略离港所用的时间)?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com