题目列表(包括答案和解析)
）与l2:y=
x+
相交于点P,直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2……这样一直作下去，可得到一系列点P1,Q1,P2,Q2,….点Pn（n=1,2,…）的横坐标构成数列｛xn｝. 
（Ⅰ）证明:xn+1－1=
（xn－1）,n∈N*;
（Ⅱ）求数列｛xn｝的通项公式；
（Ⅲ）比较2|PPn|2与4k2|PP1|2+5的大小.
如图，直线l1∶y＝kx＋1－k(k≠0，k≠±
)与l2∶y＝
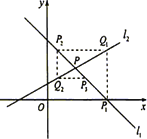
＋相交于点P．直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1、Q1、P2、Q2，…，点Pn(n＝1，2，…)的横坐标构成数列{xn}．
(Ⅰ)证明xn+1－1＝
，n∈N*；
(Ⅱ)求数列{xn}的通项公式；
(Ⅲ)比较2|PPn|2与4k2|PP1|2＋5的大小．
如图，直线l1：y＝kx＋1－k(k≠0，k≠
)与l2：y＝
x＋相交于点P，直线l1与x轴交于P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1，Q1，P2，Q2，…，点Pn(n＝1，2，…)的横坐标构成数列{xn}．
(1)证明：xn+1－1＝
(xn－1)，n∈N+；
(2)求数列{xn}的通项公式；
(3)比较2|PPn|2与4k2|PP1|2＋5的大小．
k为何值时，直线l1：3x－(k+2)y+k+5=0与l2：kx+(2k－3)y+2=0 (1)平行? (2)垂直?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com