(本小题共13分)

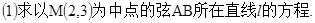
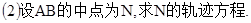
（本小题共13分）
某公司要将一批海鲜用汽车运往A城，如果能按约定日期送到，则公司可获得销售收入30万元，每提前一天送到，或多获得1万元，每迟到一天送到，将少获得1万元，为保证海鲜新鲜，汽车只能在约定日期的前两天出发，且行驶路线只能选择公路1或公路2中的一条，运费由公司承担，其他信息如表所示.

统计信息 汽车行驶 路线	不堵车的情况下到达所需时间（天）	堵车的情况下到达所需时间（天）	堵车的概率	运费（万元）
公路1	2	3		1.6
公路2	1	4		0.8

（本小题共13分）

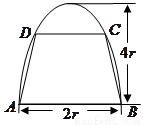如图，有一块半椭圆形钢板，其半轴长为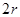，短半轴长为，计划将此钢板切割成等腰梯形的形状，下底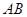是半椭圆的短轴，上底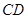的端点在椭圆上，记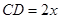，梯形面积为．

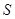（I）求面积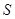以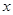为自变量的函数式，并写出其定义域；

（II）求面积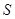的最大值．

（本小题共13分）
在平面直角坐标系xOy中，经过点（0, 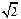）且斜率为k的直线l与椭圆 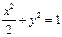有两个不同的交点P和Q.
(Ⅰ)求k的取值范围；
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k，使得向量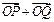与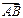共线？如果存在，求出k的值；如果不存在，请说明理由.

（本小题共13分）

为了调查某厂2000名工人生产某种产品的能力，随机抽查了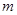位工人某天生产该产品的数量，产品数量的分组区间为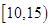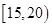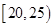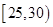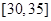，，,，,频率分布直方图如图所示．已知生产的产品数量在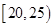之间的工人有6位．

（Ⅰ）求；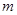

（Ⅱ）工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，则这2位工

人不在同一组的概率是多少？