
题目列表(包括答案和解析)
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.[来源:学,科,网Z,X,X,K]
【解析】第一问解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
(11)由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
设向量 .
.
(Ⅰ)求 ;
;
(Ⅱ)若函数 ,求
,求 的最小值、最大值.
的最小值、最大值.
【解析】第一问中,利用向量的坐标表示,表示出数量积公式可得


第二问中,因为 ,即
,即 换元法
换元法
令 得到最值。
得到最值。
解:(I)



(II)由(I)得:
令
 .
.
 时,
时,
已知向量 =(
=( ),
), =(
=(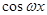 ,
,
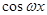 ),其中(
),其中(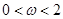 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得 ,……11分故
,……11分故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com