
题目列表(包括答案和解析)
关于
x的不等式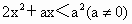 ,提供四个解集:①当a>0时,
,提供四个解集:①当a>0时,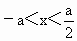 ,②当a>0时,
,②当a>0时,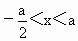 ,③当a<0时,
,③当a<0时,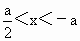 ,④当a<0时,
,④当a<0时,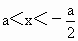 ,那么原不等式的解集为
,那么原不等式的解集为
[
]|
A .②或③ |
B .①或③ |
C .①或④ |
D .②或④ |
关于x的不等式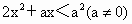 ,提供四个解集:①当a>0时,
,提供四个解集:①当a>0时,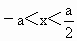 ,②当a>0时,
,②当a>0时,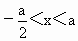 ,③当a<0时,
,③当a<0时,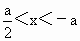 ,④当a<0时,
,④当a<0时,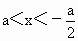 ,那么原不等式的解集为
,那么原不等式的解集为
[ ]
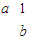 )有特征值λ1=2及对应的一个特征向量
)有特征值λ1=2及对应的一个特征向量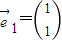 .
.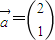 ,求
,求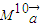 .
.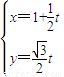 (t为参数),曲线C1:
(t为参数),曲线C1: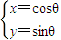 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的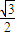 倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①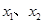 、
、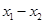 是定义域中的数时,有
是定义域中的数时,有 ;
;
②
 是定义域中的一个数);
是定义域中的一个数);
③当 时,
时, .
.
(1)判断 与
与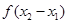 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为 时,
时,
①求 的值;②求不等式
的值;②求不等式 的解集.
的解集.
已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①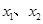 、
、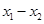 是定义域中的数时,有
是定义域中的数时,有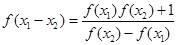 ;
;
②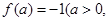
 是定义域中的一个数);
是定义域中的一个数);
③当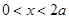 时,
时,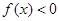 .
.
(1)判断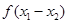 与
与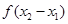 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在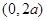 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为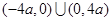 时,
时,
①求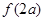 的值;②求不等式
的值;②求不等式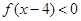 的解集.
的解集.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com