某公司是否对某一项目投资，由甲、乙、丙三位决策人投票决定，他们三人都有“同意”、“中立”、“反对”三类票各一张，投票时，每人必须且只能投一张票，每人投三类票中的任何一类的概率都是，他们的投票相互没有影响。规定：若投票结果中至少有2张“同意”票，则决定对该项目投资，否则放弃投资。（Ⅰ）求此公司决定对该项目投资的概率；（Ⅱ）求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率．

①;

②;    ③;

④,能成为P的算式的是(    )

A.①②             B.②③              C.③④                D.①④

为了了解某市工人开展体育活动的情况，拟采用分层抽样的方法从A，B，C三个区中抽取7个工厂进行调查，已知A，B，C区中分别有18，27，18个工厂

（Ⅰ）从A，B，C区中分别抽取的工厂个数；

（Ⅱ）若从抽取的7个工厂中随机抽取2个进行调查结果的对比，计算这2个工厂中至少有1个来自A区的概率.

【解析】本试题主要考查了统计和概率的综合运用。

第一问工厂总数为18+27+18=63，样本容量与总体中的个体数比为7/63=1/9…3分

所以从A，B，C三个区中应分别抽取的工厂个数为2，3，2。

第二问设A₁，A₂为在A区中的抽得的2个工厂，B₁，B₂­，B₃为在B区中抽得的3个工厂，

C₁，C₂为在C区中抽得的2个工厂。

这7个工厂中随机的抽取2个，全部的可能结果有1/2*7*6=32种。

随机的抽取的2个工厂至少有一个来自A区的结果有A₁，A₂），A₁，B₂），A₁，B₁），

A₁，B₃）A₁，C₂），A₁，C₁）， …………9分

同理A₂还能给合5种，一共有11种。  

所以所求的概率为p=11/21

（本小题满分12分）

第4届湘台经贸洽谈交流会于2011年6月在我市举行 ，为了搞好接待工作，大会组委会在

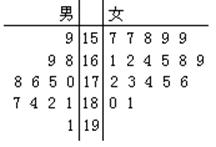
某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎

叶图（单位：cm）：若身高在175cm以上（包括175cm）定义为“高个子”， 身高在175cm

以下（不包括175cm）定义为“ 非高个子 ”，且只有“女高个子”才担任“礼仪小姐”。（I）如

果用分层抽样的方法从“高个子”中和“非高个子”中提取5人，再从这5人中选2人，那么至

少有一人是“高个子”的概率是多少？（II）若从所有“高个子”中选3名志愿者，用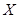表示所

选志愿者中能担任“礼仪小姐”的人数，试写出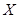的分布列，并求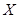的数学期望。