练习册

  • 练习册
  • 试题
    10．若用表示已知条件和已学过的定义.定理等.用表示要证明的结论.则分析法解题过程的流程图可表示为 ． 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)

    从某校高三年级900名学生中随机抽取了名测量身高，据测量被抽取的学生的身高全部介于和之间，将测量结果按如下方式分成八组：第一组,第二组…第八组，右图是按上述分组方法得到的条形图．

     （1）根据已知条件填写下面表格：

    组 别

    1

    2

    3

    4

    5

    6

    7

    8

    样本数

     

     

     

     

     

     

     

     

    （2）估计这所学校高三年级900名学生中，身高在以上（含）的人数；

    （3）在样本中，若第二组有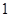人为男生，其余为女生，第七组有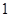人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，用表示实验小组中男同学的人数，求的分布列及期望

     

    ．

     

     

     

     

     

    查看答案和解析>>

    已知命题p：
    x2
    m-1
    +
    y2
    m-4
    =1    表示双曲线，命题q：
    x2
    m-2
    +
    y2
    4-m
    =1    表示椭圆．
    （1）若命题p为真命题，求实数m的取值范围．
    （2）判断命题p为真命题是命题q为真命题的什么条件（请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个）．

    查看答案和解析>>

    如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
    （Ⅰ）求异面直线AB和C1D所成的角（用反三角函数表示）；
    （Ⅱ）若E为AB上一点，试确定点E在AB上的位置，使得A1E⊥C1D；
    （Ⅲ）在（Ⅱ）的条件下，求点D到平面B1C1E的距离．

    查看答案和解析>>

    数列{an}和数列{bn}（n∈N*）由下列条件确定：
    （1）a1＜0，b1＞0；
    （2）当k≥2时，ak与bk满足如下条件：当
    ak-1+bk-1
    2
    ≥0时，ak=ak-1，bk=
    ak-1+bk-1
    2
    ；当
    ak-1+bk-1
    2
    ＜0时，ak=
    ak-1+bk-1
    2
    ，bk=bk-1．
    解答下列问题：
    （Ⅰ）证明数列{ak-bk}是等比数列；
    （Ⅱ）记数列{n（bk-an）}的前n项和为Sn，若已知当a＞1时，
    lim
    n→∞
    n
    an
    =0，求
    lim
    n→∞
    Sn    ．
    （Ⅲ）m（n≥2）是满足b1＞b2＞…＞bn的最大整数时，用a1，b1表示n满足的条件．

    查看答案和解析>>

    （2013•怀化三模）若某地区每年各个月份降水量发生周期变化．现用函数f（n）=100[Acos（ωn+
    23
    π）+m]近似地刻画．其中：正整数n表示月份且n∈[1，12]，例如n=1时表示1月份，A和m是正整数，ω＞0．统计发现，该地区每年各个月份降水量有以下规律：
    ①各年相同的月份，该地区降水量基本相同；
    ②该地区降水量最大的8月份和最小的12月份相差约400ml；
    ③2月份该地区降水量约为100ml，随后逐月递增直到8月份达到最大．
    （1）试根据已知信息，确定一个符合条件的f（n）的表达式；
    （2）一般地，当该地区降水量超过400 ml时，该地区进入了一年中的“汛季”，那么一年中的哪几个月是该地区的“汛季”？请说明理由．

    查看答案和解析>>


    同步练习册答案