(本小题满分12分）

如图所示，四边形ABCD为矩形，点M是BC的中点，CN=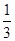CA,用向量法证明：

（1）D、N、M三点共线；（2）若四边形ABCD为正方形，则DN=BN.

（本小题满分12分）如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点。已知AB=3米，AD=2米。

 （I）设（单位：米），要使花坛AMPN的面积大于32平方米，求的取值范围；

 （II）若（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。

（本小题满分12分）如图所示，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.

（1）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

（2）求证：无论点E在BC边的何处，都有PE⊥AF；

（3）当BE为何值时，PA与平面PDE所成角的大小为45°.

（本小题满分12分）

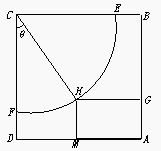
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示)，ABCD是一块边长为50 m的正方形地皮，扇形CEF是运动场的一部分，其半径为40 m，矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，H在   上。设矩形AGHM的面积为S，∠HCF=θ，请将S表示为θ的函数，并指出当点H在    的何处时，该健身室的面积最大，最大面积是多少？ 

（本小题满分12分）如图所示，已知PA⊥矩形ABCD所在平面，

M，N分别是AB，PC的中点.

（1）求证：MN⊥CD；

（2）若∠PDA=45°.求证：MN⊥平面PCD.