
题目列表(包括答案和解析)
(本小题满分14分)等比数列 中,
中,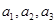 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且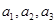 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
|
|
第一列 |
第二列 |
第三列 |
|
第一行 |
3 |
2 |
10 |
|
第二行[来 |
6 |
4 |
14 |
|
第三行 |
9 |
8 |
18 |
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列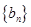 满足
满足 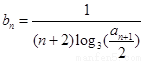 ,记数列
,记数列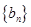 的前n项和为
的前n项和为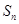 ,证明
,证明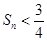
(本小题满分14分)等比数列 中,
中, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且
 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
|
|
第一列 |
第二列 |
第三列 |
|
第一行 |
3 |
2 |
10 |
|
第二行 |
6 |
4 |
14 |
|
第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足
 ,记数列
,记数列 的前n项和为
的前n项和为 ,证明
,证明
(本小题满分12分)
等比数列![]() 中,
中,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足:
满足:![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(本小题满分12分)
等比数列![]() 中,
中,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足:
满足:![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
(本小题满分14分)2010年上海世博会举办时间为2010年5月1日~10月31日(共184天).福建馆位于上海世博会中国省区市馆东南区域,以“海西”为参博的核心元素,主题为“潮涌海西,魅力福建” .此次世博会福建馆招募了60名志愿者,某高校有13人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所学院(这5所学院编号为1~5号),人员分布如图所示.
若从这13名入选者中随机抽出3人.
(Ⅰ)求这3人所在学院的编号正好成等比数列的概率;
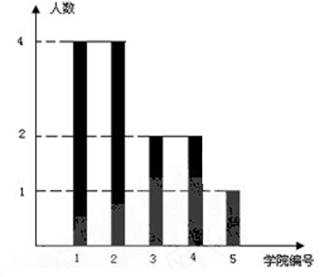
(Ⅱ)求这3人中中英文讲解员人数的分布列及数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com