
题目列表(包括答案和解析)
设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
A、y=12+3sin
| ||||
B、y=12+3sin(
| ||||
C、y=12+3sin
| ||||
D、y=12+3sin(
|
| t | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
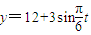 ,t∈[0,24]
,t∈[0,24]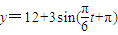 ,t∈[0,24]
,t∈[0,24]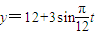 ,t∈[0,24]
,t∈[0,24]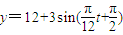 ,t∈[0,24]
,t∈[0,24]| t | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
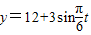 ,t∈[0,24]
,t∈[0,24]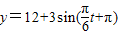 ,t∈[0,24]
,t∈[0,24]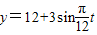 ,t∈[0,24]
,t∈[0,24]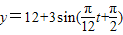 ,t∈[0,24]
,t∈[0,24]设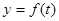 是某港口水的深度
是某港口水的深度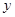 (米)关于时间
(米)关于时间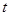 (时)的函数,其中
(时)的函数,其中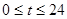 ,下表是该港口某一天从0时至24时记录的时间
,下表是该港口某一天从0时至24时记录的时间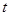 与水深
与水深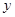 的关系:
的关系:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经观察,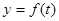 可以近似看成
可以近似看成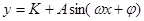 的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( )
的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( )
(A)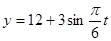 ,
,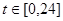 (B)
(B)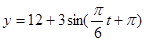 ,
,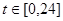
(C)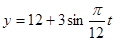 ,
,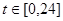 (D)
(D)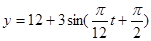 ,
,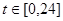
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com