
题目列表(包括答案和解析)
已知三个函数模型: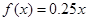 ,
,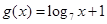 ,
,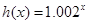 ,当
,当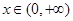 ,随
,随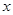 的增大,三个函数中的增长速度越来越快的是(
)
的增大,三个函数中的增长速度越来越快的是(
)
A.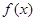 B.
B.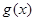 C.
C. D.
D.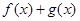
已知三个函数模型: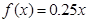 ,
,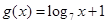 ,
,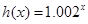 ,当
,当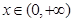 ,随
,随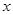 的增大,三个函数中的增长速度越来越快的是( )
的增大,三个函数中的增长速度越来越快的是( )
A.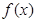 B.
B.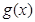 C.
C.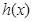 D.
D.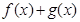
身高x/cm | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
体重y/kg | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(1)画出散点图.
(2)能否建立恰当的函数模型使它能比较近似地反映这个地区未成年男性体重y(kg)与身高x(cm)的函数关系?试写出这个函数模型的解析式.
(3)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为瘦,那么这个地区一名身高为175 cm,体重为78 kg的在校男生的体重是否正常?
| A.f(x) | B.g(x) | C.h(x) | D.f(x)+g(x) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com