已知函数

   （1）若的极值点，求实数a的值；

   （2）若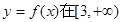上为增函数，求实数a的取值范围；

   （3）当有实根，求实数b的最大值。

【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间，求解参数的取值范围，以及利用函数与方程的思想求解参数b的最值。

某校从参加高三年级理科综合物理考试的学生中随机抽出名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；

（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的

平均分；

（Ⅲ）若从名学生中随机抽取人，抽到的学生成绩在记分，在记分，

在记分，用表示抽取结束后的总记分，求的分布列和数学期望.

【解析】（1）中利用直方图中面积和为1，可以求解得到分数在内的频率为

（2）中结合平均值可以得到平均分为：

（3）中用表示抽取结束后的总记分x, 学生成绩在的有人，在的有人，在的有人,结合古典概型的概率公式求解得到。

(Ⅰ)设分数在内的频率为，根据频率分布直方图，则有，可得，所以频率分布直方图如右图.……4分

（求解频率3分，画图1分）

（Ⅱ）平均分为：……7分

（Ⅲ）学生成绩在的有人，在的有人，

在的有人.并且的可能取值是.    ………8分

则；； ；

；.（每个1分）

所以的分布列为

…………………13分

    对于定义在上的函数，若存在，对任意的，都有或者，则称为函数在区间上的“下确界”或“上确界”．

（Ⅰ）求函数在上的“下确界”；

（Ⅱ）若把“上确界”减去“下确界”的差称为函数在上的“极差”， 试求函数在上的“极差”；

（Ⅲ）类比函数的“极差”的概念， 请求出在上的“极差”．

已知函数

（I）     讨论f（x）的单调性；

（II）   设f（x）有两个极值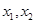点若过两点的直线I与x轴的交点在曲线上，求α的值。

【解析】本试题考查了导数在研究函数中的运用。第一就是三次函数，通过求解导数，求解单调区间。另外就是运用极值的概念，求解参数值的运用。

【点评】试题分为两问，题面比较简单，给出的函数比较常规，，这一点对于同学们来说没有难度但是解决的关键还是要看导数的符号的实质不变，求解单调区间。第二问中，运用极值的问题，和直线方程的知识求解交点，得到参数的值。

（1）