
题目列表(包括答案和解析)
 如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+
如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+| y2 |
| m |
| 2 |
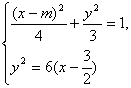 (其中θ为参数)和抛物线
(其中θ为参数)和抛物线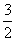 (其中t为参数).
(其中t为参数).(1)是否存在这样的m值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
(2)当m取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
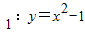 (|x|≥1)和曲线C2:
(|x|≥1)和曲线C2: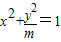 (y≤0,m>0)“合成”的,直线l与曲线C1相切于点M,与曲线C2相切于点N,记点M的横坐标为t(t>1),其中A(-1,0),B(1,0).
(y≤0,m>0)“合成”的,直线l与曲线C1相切于点M,与曲线C2相切于点N,记点M的横坐标为t(t>1),其中A(-1,0),B(1,0). 时,求m的值和点N的坐标;
时,求m的值和点N的坐标;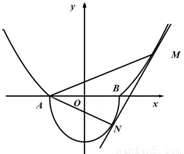
 己知点F为抛物线C:y2=x的焦点,斜率为1的直线l交抛物线于不同两点P,Q.以F为圆心,以FP,FQ为半径作圆,分别交x轴负半轴于M,N,直线PM,QN交于点T.
己知点F为抛物线C:y2=x的焦点,斜率为1的直线l交抛物线于不同两点P,Q.以F为圆心,以FP,FQ为半径作圆,分别交x轴负半轴于M,N,直线PM,QN交于点T.| S1S2 | S3 |
 取得最小值,并求出取到最小值时直线l的方程.
取得最小值,并求出取到最小值时直线l的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com