练习册

  • 练习册
  • 试题
    3．幂函数的性质 从上图可以观察到幂函数的特征如下: 定义域 值域 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 时.增 增 增 时.减 时.减 时.减 定点 (1,1) (0,0) (1,1) (0,0) (1,1) (0,0) (1,1) (0,0) (1,1) 结合以上特征得幂函数的性质如下: (1)所有的幂函数在都有定义.并且图象都通过点(1,1), (2)如果.则幂函数的图象过原点.并且在区间上为增函数, (3)如果.则幂函数的图象在区间上是减函数.在第一象限内.当从右边趋向于原点时.图象在轴右方无限地逼近轴.当趋向于时.图象在轴上方无限地逼近轴, (4)当为奇数时.幂函数为奇函数.当为偶函数.幂函数为偶函数. 【查看更多】

     

    题目列表(包括答案和解析)

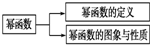    精英家教网如图所示的框图中“幂函数的定义”“幂函数的图象与性质”与“幂函数”的关系是（　　）
    A、并列关系B、从属关系C、包含关系D、交叉关系

    查看答案和解析>>

    已知有5个幂函数的图象如图，其中它们的指数来源于集合{-
    2
    5
    ，
    2
    5
    ，-
    1
    2
    ，
    5
    3
    ，-
    5
    2
    ，
    5
    2
    }    ，则其指数从（a）到（e）依次为
    2
    5
    ，-
    2
    5
    ，-
    1
    2
    ，
    5
    2
    ，-
    5
    2
    2
    5
    ，-
    2
    5
    ，-
    1
    2
    ，
    5
    2
    ，-
    5
    2
    ．

    查看答案和解析>>

    （本小题满分14分）我们把叫做幂函数。幂函数的一个性质是，当时，在上是增函数；当时，在上是减函数。     设幂函数

       （1）若，证明：当时，有；

       （2）若，对任意的，证明；

       （3）在（2）的条件下，证明：

    查看答案和解析>>

    如何利用幂函数的图像来归纳其性质？

    查看答案和解析>>

    下图表示某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系：y＝ta，有以下叙述：

    ①这个幂函数的指数为3；

    ②第5个月时，浮萍的面积就会超过100 m2；

    ③浮萍从10 m2蔓延到80 m2需要经过2.5个月；

    ④浮萍每月增加的面积都相等．

    其中正确的序号是

    [　　]
    A．

    ①②③

    B．

    ①②③④

    C．

    ②③④

    D．

    ①②

    查看答案和解析>>


    同步练习册答案