题目列表(包括答案和解析)
定义在R上的函数f(x)满足：
①对任意x，y∈R，都有f(x)＋f(y)=f(x＋y)；
②当x＜0时，有f(x)＜0．
(Ⅰ)根据函数奇偶性的定义，判断f(x)的奇偶性；
(Ⅱ)根据函数单调性的定义，判断f(x)的单调性；
(Ⅲ)若f(k·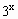
)＋f(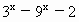
)＜0对任意x∈R恒成立；求实数k的取值范围．
（Ⅳ）求证：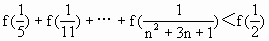
函数的单调性和奇偶性是函数的两个重要性质，你能说说这两条性质的区别吗？函数的奇偶性反映在函数图象上表现为图象的对称性，你能说出奇偶性与对称性之间的对应关系吗？用定义来判断函数的奇偶性的一般步骤是什么？请你总结一下函数的奇偶性的性质．
| A．函数的单调区间可以是函数的定义域 |
| B．函数的多个单调增区间的并集也是其单调增区间 |
| C．具有奇偶性的函数的定义域定关于原点对称 |
| D．关于原点对称的图象一定是奇函数的图象 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com