
题目列表(包括答案和解析)
下面关于 的判断:
的判断:
 与
与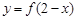 的图象关于直线
的图象关于直线 对称;
对称;
若 为偶函数,且
为偶函数,且 ,则
,则 的图象关于直线
的图象关于直线 对称;
对称;
设函数 ,且
,且 ,
, ,
, ,若
,若 ,则
,则
函数 ,
, ,
, ,
, ,存在
,存在 ,
, ,使得
,使得
 .
.
其中正确的判断是____ _____(把你认为正确的判断都填上)
下面关于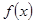 的判断:
的判断: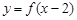 与
与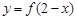 的图象关于直线
的图象关于直线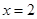 对称;
对称;
若 为偶函数,且
为偶函数,且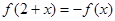 ,则
,则 的图象关于直线
的图象关于直线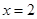 对称;
对称;
设函数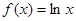 ,且
,且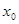 ,
,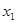 ,
,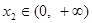 ,若
,若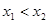 ,则
,则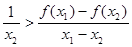
函数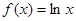 ,
,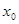 ,
,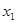 ,
,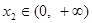 ,存在
,存在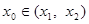 ,
,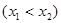 ,使得
,使得 .
.
其中正确的判断是____ _____(把你认为正确的判断都填上)
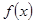 的判断:
的判断: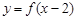 与
与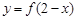 的图象关于直线
的图象关于直线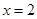 对称;
对称;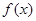 为偶函数,且
为偶函数,且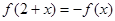 ,则
,则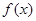 的图象关于直线
的图象关于直线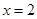 对称;
对称;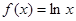 ,且
,且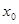 ,
,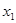 ,
,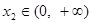 ,若
,若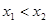 ,则
,则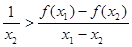
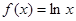 ,
,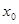 ,
,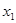 ,
,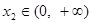 ,存在
,存在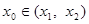 ,
,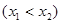 ,使得
,使得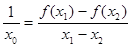 .
.下面关于![]() 的判断:
的判断:
① ![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
② 若![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③ 设函数![]() ,且
,且![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,
则![]()
④ 函数![]() ,
,![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,
,![]() ,
,
使得![]()
⑤设函数![]() ,
,![]() .对于
.对于![]()
![]() ,总
,总![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为![]() .
.
其中正确的判断是 (把你认为正确的判断都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com