
题目列表(包括答案和解析)
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 2s |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
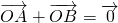 ③O是直线AB上所有点中到线段AB两个端点的距离的平方和最小的点.由此推广到三角形,设△ABC的重心为G,我们得到如下猜想:
③O是直线AB上所有点中到线段AB两个端点的距离的平方和最小的点.由此推广到三角形,设△ABC的重心为G,我们得到如下猜想: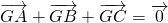
对于各项均为整数的数列![]() ,如果
,如果![]() (
(![]() =1,2,3,…)为完全平方数(即能表示为一个整数的平方的数,例如4是完全平方数、3不是完全平方数),则称数列
=1,2,3,…)为完全平方数(即能表示为一个整数的平方的数,例如4是完全平方数、3不是完全平方数),则称数列![]() 具有“
具有“![]() 性质”.不论数列
性质”.不论数列![]() 是否具有“
是否具有“![]() 性质”,如果存在与
性质”,如果存在与![]() 不是同一数列的
不是同一数列的![]() ,且
,且![]() 同时满足下面两个条件:①
同时满足下面两个条件:①![]() 是
是![]() 的一个排列;②数列
的一个排列;②数列![]() 具有“
具有“![]() 性质”,则称数列
性质”,则称数列![]() 具有“变换
具有“变换![]() 性质”.下面三个数列:①数列
性质”.下面三个数列:①数列![]() 的前
的前![]() 项和
项和![]() ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“![]() 性质”的为 ;具有“变换
性质”的为 ;具有“变换![]() 性质”的为 .
性质”的为 .
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
.
(1)求证: ;
;
(2)若四边形ABCD是正方形,求证 ;
;
(3)在(2)的条件下,求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中,利用由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF
第二问中,由线面垂直得到线线垂直。四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



第三问中,设正方形ABCD的边长为x,则在
在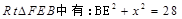

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
证明:(1)由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF

(2) 四边形ABCD是正方形
四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



(3)设正方形ABCD的边长为x,则在
在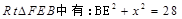

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
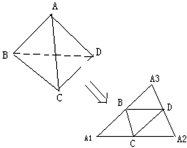 (2006•黄浦区二模)已知四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,得到△A1A2A3(如图),试写出四面体ABCD应满足的一个性质:
(2006•黄浦区二模)已知四面体ABCD,沿棱AB、AC、AD剪开,铺成平面图形,得到△A1A2A3(如图),试写出四面体ABCD应满足的一个性质:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com