
题目列表(包括答案和解析)
已知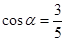 ,
,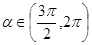 ,求
,求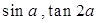 的值
的值
【解析】本试题主要考查了三角函数的二倍角公式的运用。利用同角三角函数关系式可知
 ,所以
,所以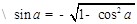
 ,再利用二倍角正切公式
,再利用二倍角正切公式
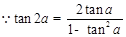 得到结论。
得到结论。
解:(Ⅰ)
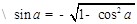
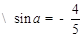

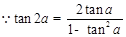
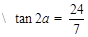
已知函数 。求函数
。求函数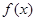 的单调递增区间和最小值;
的单调递增区间和最小值;
【解析】第一问中利用三角函数的二倍角公式求解运算得到性质。利用二倍角公式求解
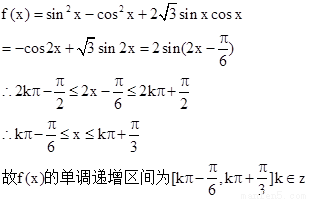
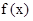 的最小值为-2
的最小值为-2
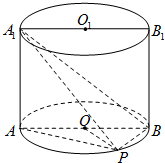 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.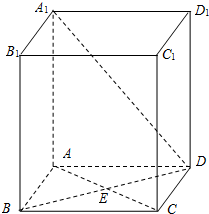 (2006•静安区二模)如图所示,已知正四面体ABCD的棱长为2,点E为棱AD的中点,求:
(2006•静安区二模)如图所示,已知正四面体ABCD的棱长为2,点E为棱AD的中点,求:| π |
| 5 |
| π |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com