已知中心在原点O，焦点F₁、F₂在x轴上的椭圆E经过点C（2，2），且抛物线的焦点为F₁.

（Ⅰ）求椭圆E的方程；

（Ⅱ）垂直于OC的直线l与椭圆E交于A、B两点，当以AB为直径的圆P与y轴相切时，求直线l的方程和圆P的方程.

【解析】本试题主要考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。第一问中，设出椭圆的方程，然后结合抛物线的焦点坐标得到，又因为，这样可知得到。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到

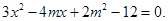，再利用可以结合韦达定理求解得到m的值和圆p的方程。

解：(Ⅰ)设椭圆E的方程为

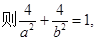①………………………………1分

  ②………………２分

  ③       由①、②、③得a²=12,b²=6…………3分

所以椭圆E的方程为…………………………4分

(Ⅱ)依题意，直线OC斜率为1，由此设直线l的方程为y=-x+m，……………5分

 代入椭圆E方程，得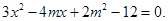…………………………6分

………………………7分

、………………8分

………………………9分

……………………………10分

    当m=3时，直线l方程为y=-x+3，此时，x₁ +x₂=4，圆心为（2，1），半径为2，

圆P的方程为（x-2）²+(y-1)²=4；………………………………11分

同理，当m=－3时，直线l方程为y=-x－3，

圆P的方程为（x+2）²+(y+1)²=4

 

（本小题满分12分）

为了解某班学生喜欢打篮球是否与性别有关，对该班50人进行了问卷调查得到了如下的列联表：

	喜欢打篮球	不喜欢打篮球	合 计
男 生		5
女 生	10
合 计			50

已知在全部50人中随机抽取1人抽到喜欢打篮球的学生的概率为0.6。

（Ⅰ）请将上面的列联表补充完整；

（Ⅱ）是否有99％的把握认为喜欢打篮球与性别有关？说明你的理由；

（Ⅲ）已知不喜欢打篮球的5位男生中，喜欢踢足球，喜欢打羽毛球，喜欢打乒乓球，现在从这5位男生中选取3位进行其他方面的调查，求和不全被选中的概率。

附:1．

2．在统计中，用以下结果对变量的独立性进行判断：

(1)当时,没有充分的证据判定变量有关联，可以认为变量是没有关联的；

(2)当时，有90%的把握判定变量有关联；

(3)当时，有95%的把握判定变量有关联；

(4)当时，有99%的把握判定变量有关联。

 

 

 

 

 

（本小题满分12分）

为了解某班学生喜欢打篮球是否与性别有关，对该班50人进行了问卷调查得到了如下的列联表：

	喜欢打篮球	不喜欢打篮球	合 计
男 生		5
女 生	10
合 计			50

已知在全部50人中随机抽取1人抽到喜欢打篮球的学生的概率为0.6。

（Ⅰ）请将上面的列联表补充完整；

（Ⅱ）是否有99％的把握认为喜欢打篮球与性别有关？说明你的理由；

（Ⅲ）已知不喜欢打篮球的5位男生中，喜欢踢足球，喜欢打羽毛球，喜欢打乒乓球，现在从这5位男生中选取3位进行其他方面的调查，求和不全被选中的概率。

附:1．

2．在统计中，用以下结果对变量的独立性进行判断：

(1)当时,没有充分的证据判定变量有关联，可以认为变量是没有关联的；

(2)当时，有90%的把握判定变量有关联；

(3)当时，有95%的把握判定变量有关联；

(4)当时，有99%的把握判定变量有关联。