（本小题满分12分）

某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30.第6小组的频数是7.

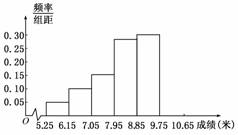(1) 求这次铅球测试成绩合格的人数；

(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名，记表示两人中成绩不合格的人数，求的分布列及数学期望；

(3) 经过多次测试后，甲成绩在8～10米之间，乙成绩在9.5～10.5米之间，现甲、乙各投掷一次，求甲比乙投掷远的概率.

（本小题满分12分）某校高二年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：

分组	频数	频率
[85,95)	①	②
[95,105)		0.050
[105,115)		0.200
[115,125)	12	0.300
[125,135)		0.275
[135,145)	4	③
[145,155)		0.050
合计		④

 

(1)根据上面图表，①②③④处的数值分别为________、________、________、________；
(2)在所给的坐标系中画出[85,155]的频率分布直方图；
(3)根据题中信息估计总体平均数，并估计总体落在[129,155]中的频率．

（本小题满分12分）

某市为了对学生的数理（数学与物理）学习能力进行分析，从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本，分数频数分布如下表：

等级得分
人数	3	17	30	30	17	3

（Ⅰ）如果以能力等级分数大于4分作为良好的标准，从样本中任意抽取２名学生，求恰有１名学生为良好的概率；

（Ⅱ）统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值为1.5）作为代表：

(ⅰ)据此，计算这100名学生数理学习能力等级分数的期望及标准差(精确到0.1)；

(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在范围内的人数 ．

（Ⅲ）从这10000名学生中任意抽取5名同学，

他们数学与物理单科学习能力等级分

数如下表：

（ⅰ）请画出上表数据的散点图；

（ⅱ）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程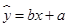（附参考数据：）

 

 

 

（本小题满分12分）

一个几何体是由圆柱和三棱锥组合而成，点、、在圆的圆周上，其正（主）视图、侧（左）视图的面积分别为10和12，如图所示，其中，，，．

（1）求证：；

（2）求二面角的平面角的大小．

 

（本小题满分12分）高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：

分组	频数	频率
	①	②
		0.050
		0.200
	12	0.300
		0.275
	4	③
		0.050
合 计		④

（1）根据上面图表，①、②、③、④处的数值分别是多少？

（2）在坐标系中画出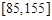的频率分布直方图；

（3）根据题中信息估计总体平均数，并估计总体落在中的概率。