题目列表(包括答案和解析)
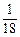x2－
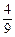x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)
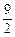）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；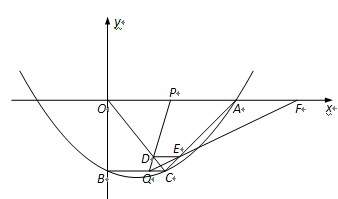
解答题
已知a，b，c均为实数，函数f(x)＝ax2＋bx＋c与g(x)＝ax＋b，且当－1≤x≤1时，恒有|f(x)|≤1．证明：(1)|c|≤1；(2)|g(x)|≤2．
对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称点(x0，x0)为函数f(x)的不动点．
(Ⅰ)已知函数f(x)＝ax2＋bx－b(a≠0)有不动点(1，1)和(－3，－3)，求a、b的值；
(Ⅱ)若对于任意实数b，函数f(x)＝ax2＋bx－b总有两个相异的不动点，求实数a的取值范围；
(Ⅲ)(理)若定义在实数集R上的奇函数g(x)存在(有限的)n个不动点，求证：n必为奇数．
| |||||||||||
已知二次函数f(x)＝ax2＋bx＋c(a＞0)的图象与x轴有两个不同点的公共点，若f(c)＝0，且0＜x＜c时，f(x)＞0．
(Ⅰ)试比较
与c的大小；
(Ⅱ)证明：－2＜b＜－1；
(Ⅲ)当c＞1，t＞0时，求证：
＋
＋
＞0．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋2．
，且g(x)在区间(0，2]上为减函数，求实数a的取值范围．