
题目列表(包括答案和解析)
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式![]() .
.
解:∵![]() ,
,
∴![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() (2)
(2)![]()
解不等式组(1),得![]() ,
,
解不等式组(2),得![]() ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m ![]()
![]()
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式![]() .
.
解:∵![]() ,
,
∴![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() (2)
(2)![]()
解不等式组(1),得![]() ,
,
解不等式组(2),得![]() ,
,
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
问题:求分式不等式![]() 的解集.
的解集.
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
当0<x≤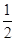 时,4x<logax,则a的取值范围是
时,4x<logax,则a的取值范围是
(A)(0,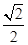 )
(B)(
)
(B)(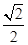 ,1) (C)(1,
,1) (C)(1,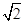 ) (D)(
) (D)(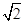 ,2)
,2)
【解析】当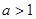 时,显然不成立.若
时,显然不成立.若 时
时
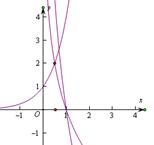
当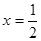 时,
时,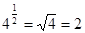 ,此时对数
,此时对数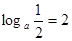 ,解得
,解得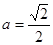 ,根据对数的图象和性质可知,要使
,根据对数的图象和性质可知,要使 在
在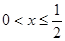 时恒成立,则有
时恒成立,则有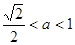 ,如图选B.
,如图选B.
(1)他们每人都至少解出1题;
(2)在没有解出第1题的那些学生中,解出第2题的是解出第3题的人数的2倍;
(3)只解出第1题的比余下的学生中解出第1题的多1人;
(4)只解出1道题的学生中,有一半没有解出第1题.
试问有多少学生只解出第2题?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com