
题目列表(包括答案和解析)
设A={x||x-1|<2},B={x|![]() >0},则A∩B等于
>0},则A∩B等于
A.{x|-1<x<3} B.{x|x<0或x>2}
C.{x|-1<x<0} D.{x|-1<x<0或2<x<3}
本题考查含绝对值不等式、分式不等式的解法及集合的运算.在进行集合运算时,把解集标在数轴上,借助图形可直观求解.
 树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
树林的边界是直线l(如图所示),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于l的垂线AC上的点A点B点处,AB=BC=a(a为正常数),若兔子沿AD方向以速度2μ向树林逃跑,同时狼沿线段BM(M∈AD)方向以速度μ进行追击(μ为正常数),若狼到达M处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.已知椭圆![]() 的离心率为
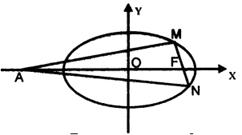
的离心率为![]() ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且![]() ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当![]() 时.,
时.,![]() ;
;
(2)若当![]() 时有
时有![]() ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当![]() 的值为6
的值为6![]() 时, 求出直线MN的方程.
时, 求出直线MN的方程.
已知函数![]()
(1)若![]() 有极值,求b的取值范围;
有极值,求b的取值范围;
(2)若![]() 在
在![]() 处取得极值时,当
处取得极值时,当![]() 恒成立,求c的取值范围;
恒成立,求c的取值范围;
(3)若![]() 在
在![]() 处取得极值时,证明:对[-1,2]内的任意两个值
处取得极值时,证明:对[-1,2]内的任意两个值![]() 都有
都有![]() .
.
(12分)已知函数![]()
(1)若![]() 有极值,求b的取值范围;
有极值,求b的取值范围;
(2) 若![]() 在
在![]() 处取得极值时,当
处取得极值时,当![]() 恒成立,求c的取值范围;
恒成立,求c的取值范围;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com