
题目列表(包括答案和解析)
式子________称为函数f(x)从x1到x2的平均变化率(average rate of change).
习惯上用Δx表示________,即Δx=________,可把Δx看作是相对于x1的一个“增量”,可用x1+Δx代替x2,类似地,Δf=________.于是,平均变化率可以表示为________.
| π |
| 4 |
| ||
| 2 |
| 2 |
| x |
| a2x+a2-2 | 2x-1 |
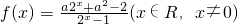 ,其中a为常数,且a<0.
,其中a为常数,且a<0.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com