
题目列表(包括答案和解析)
 某系统采用低息贷款的方式对所属企业给予扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业,以下图表给出了有关数据(将频率看作概率)
某系统采用低息贷款的方式对所属企业给予扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业,以下图表给出了有关数据(将频率看作概率)| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90) |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 54 |
| 33 |
以下说法中正确的是
① 甲乙两同学各自独立地考察了两个变量 的线性相关关系时,发现两个人对
的线性相关关系时,发现两个人对 的观测数据的平均值相等,都是
的观测数据的平均值相等,都是 。对
。对 的观测数据的平均值也相等,都是
的观测数据的平均值也相等,都是 。各自求出的回归直线分别是
。各自求出的回归直线分别是 ,则直线
,则直线 必定相交于定点
必定相交于定点 。
。
②用独立性检验(2×2列联表法)来考察两个分类变量 是否有关系时,算出的随机变量
是否有关系时,算出的随机变量 的值越大,说明“
的值越大,说明“ 有关系”成立的可能性越大。
有关系”成立的可能性越大。
③合情推理就是正确的推理。
④最小二乘法的原理是使得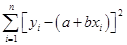 最小。
最小。
⑤用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合程度越好。
越小,说明模型的拟合程度越好。
某部门对当地城乡居民进行了主题为“你幸福吗?”的幸福指数问卷调査,并在已被问卷调查的居民中随机抽选部分居民参加“幸福职业”或“幸福愿景”的座谈会,被邀请的居民只能选择其中一场座谈会参加.已知A小区有1人,B小区有3人收到邀请并将参加一场座谈会,若A小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是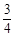 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是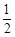 .
.
(Ⅰ)求A、B两个小区已收到邀请的人选择“幸福愿景”座谈会的人数相等的概率;
(Ⅱ)在参加“幸福愿景”座谈会的人中,记A、B两个小区参会人数的和为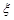 ,试求
,试求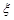 的分布列和数学期望.
的分布列和数学期望.
为抗击金融风暴,某系统决定对所属企业给予低息贷款的扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额,为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业.一下图表给出了有关数据(将频率看做概率)
(1)任抽一家所属企业,求抽到的企业等级是优秀或良好的概率;
(2)对照标准,企业进行了整改.整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com