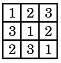
（08年全国卷Ⅰ文）将1，2，3填入3×3的方格中，要求每行、每列都没有重复数字，下面是一种填法，则不同的填写方法共有

  A．6种            B．12种         C．24种         D．48种

（07年全国卷Ⅰ理）设，集合，则 www.xkb123.com

A．1                B．               C．2              D．

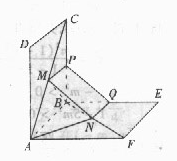
（02年全国卷理）（12分）

如图，正方形、的边长都是1，而且平面、互相垂直。点在上移动，点在上移动，若（）

（1）求的长；

（2）为何值时，的长最小；

（3）当的长最小时，求面与面所成二面角的大小。

（05年全国卷Ⅰ）（14分）

已知椭圆的中心为坐标原点O，焦点在轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，与共线。

（Ⅰ）求椭圆的离心率；

（Ⅱ）设M为椭圆上任意一点，且，证明为定值。

（05年全国卷Ⅰ文）（12分）

9粒种子分种在甲、乙、丙3个坑内，每坑3粒，每粒种子发芽的概率为，若一个坑内至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，则这个坑需要补种。

（Ⅰ）求甲坑不需要补种的概率；

（Ⅱ）求3个坑中恰有1个坑不需要补种的概率；

（Ⅲ）求有坑需要补种的概率。

（精确到）