
题目列表(包括答案和解析)
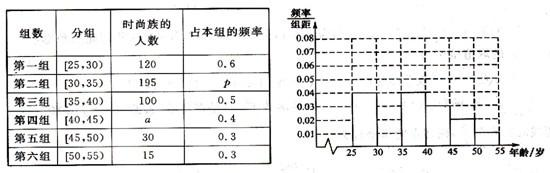
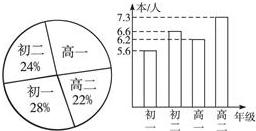 12、英才学校的四个年级学生分布如右面扇形图,通过对全体学生暑假期间所读课外书情况的调查,制成各年级读书情况的条形图如下图.已知英才学校被调查的四个年级共有学生1 500人,则
12、英才学校的四个年级学生分布如右面扇形图,通过对全体学生暑假期间所读课外书情况的调查,制成各年级读书情况的条形图如下图.已知英才学校被调查的四个年级共有学生1 500人,则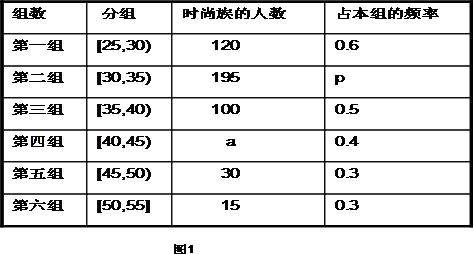
 12、甲,乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图1和如图2.
12、甲,乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图1和如图2.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com