
题目列表(包括答案和解析)
割补法是空间几何常用的一种思想方法.那么如何运用这个思想来理解以下问题:
(1)斜三棱柱的体积等于等底等高的三棱锥体积的三倍;
(2)在斜棱柱中,把与侧棱垂直的截面称作斜棱柱的直截面.斜棱柱的侧面积等于直截面的周长与侧棱长的乘积;斜棱柱的体积等于直截面的面积与侧棱长的乘积.
欧几里得算法(求两个正整数的最大公约数)是
等值算法
辗转相除法
割补法
秦九韶算法
、2002年的国际数学大会会标如右图所示,它是由四个相同的直角三解形与中间的小正方形拼成一个大正方形。若直角三角形中较小锐角为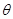 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是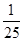 ,则
,则 的值为( )
的值为( )
A.1 B.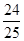 C.
C.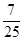 D.-
D.-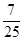
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com