练习册

  • 练习册
  • 试题
    抽象向具体转化 例7 A.B.C是球O面上三点.弧AB.AC.BC的度数分别是90°.90°.60°.求球O夹在二面角B-AO-C间部分的体积. 分析:此题难点在于空间想象.即较抽象.教师 引导学生读题:条件即∠AOB＝∠AOC＝90°.∠BOC＝60°.然后给出图形.则可想象此题意即为用刀沿60°二面角.以直径为棱将一个西瓜切下一块.求这一块西瓜的体积.(答:).问题于是变得直观具体多了. 例8 三条直线两两垂直.现有一条直线与其中两条直线都成60°角.求此直线与另外一条直线所成的角. 分析:由条件想象到长方体的三条棱也两两垂直.于是问题可以转化为如下问题:长方体一条对角线与同一顶点上的三条棱所成的角分别是60°.60°.α.求α的大小. 根据长方体的性质.有cosα+cos60°+cos60°＝1.可求得α＝45°. 立体几何的教学.关键是要调动学生的学习兴趣.让他们学会联想与转化.立体几何的许多定理.结论源自生活实际.源自平面几何.要教会学生联想实际模型.联想平面几何中已经熟悉的东西.借助可取之材来建立空间想象.加强直观教学.这样就容易让学生接受.让他们喜欢上这一门学科.从而更有效地培养他们的空间想象力.提高他们解决立体几何问题的能力. 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数y=
    1
    3
    cos(x-
    π
    7
    )    的图象为C，为了得到函数y=
    1
    3
    cos(x+
    π
    7
    )    的图象只需把C上所有的点（　　）

    查看答案和解析>>

    要得到y=cos2x的图象，只要将y=sin(2x+
    π
    4
    )    的图象向右平移最少
    7π
    8
    7π
    8
    个单位长度．

    查看答案和解析>>

    一般情况下，“下位”要素比“上位”要素更为（   ），上位要素比下位要素更为(    ),下位要素越多，结构图越(    )．

    A. 具体、复杂、抽象                    B. 具体、抽象、复杂

    C. 抽象、具体、复杂                    D. 抽象、复杂、具体

    查看答案和解析>>

    你能通过画图来表示数列1，8，16，24，32，40的和吗(参考本节例7)?

    查看答案和解析>>

    从本节的例7可以看出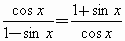，就是的一个变形．你能利用同角三角函数的基本关系推导出更多的关系式吗？

    查看答案和解析>>


    同步练习册答案