
题目列表(包括答案和解析)
定义在R上的奇函数,f(x)是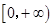 上的减函数,设a+b≤0,给出下列不等式:
上的减函数,设a+b≤0,给出下列不等式:
① f(a+b)≥0; ② f(a+b)≤0;
③ f(a)+f(b)≤f(-a)+f(-b); ④ f(a)+f(b)≥f(-a)+f(-b)。
其中正确的不等式序号是___________.
设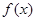 是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有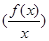 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式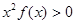 的解集是:
的解集是:
A.(一2,0)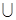 (2,+
(2,+ 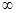 ) B.(一2,0)
) B.(一2,0)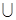 (0,2)
(0,2)
C.(-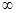 ,-2)
,-2)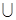 (2,+
(2,+ 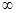 ) D.(-
) D.(-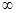 ,-2)
,-2)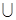 (0,2)
(0,2)
 是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式 的解集是:
的解集是:A.(一2,0) (2,+ (2,+  ) ) | B.(一2,0) (0,2) (0,2) |
C.(- ,-2) ,-2) (2,+ (2,+  ) ) | D.(- ,-2) ,-2) (0,2) (0,2) |
设![]() 是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是
是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是
A.![]()
B.[2,+∞)
C.(0,2]
D.![]()
设 是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有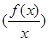 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式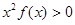 的解集是:
的解集是:
A.(一2,0)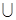 (2,+ (2,+ 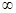 ) ) | B.(一2,0)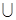 (0,2) (0,2) |
C.(-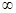 ,-2) ,-2)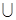 (2,+ (2,+ 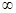 ) ) | D.(- ,-2) ,-2) (0,2) (0,2) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com