在△ABC中，内角A、B、C所对边的边长分别是a、b、c，已知c=2，C=.

(Ⅰ)若△ABC的面积等于，求a、b;

(Ⅱ)若,求△ABC的面积.

【解析】第一问中利用余弦定理及已知条件得又因为△ABC的面积等于，所以，得联立方程，解方程组得.

第二问中。由于即为即.

当时， , ,   ,  所以当时，得，由正弦定理得，联立方程组，解得,得到。

解：（Ⅰ） （Ⅰ）由余弦定理及已知条件得，………1分

又因为△ABC的面积等于，所以，得，………1分

联立方程，解方程组得.                 ……………2分

（Ⅱ）由题意得，

即.             …………2分

当时， , ,   ,          ……1分

所以        ………………1分

当时，得，由正弦定理得，联立方程组

，解得,;   所以

 [番茄花园1] （本题满分）在△ABC中，角A，B，C所对的边分别为a,b,c,设S为△ABC的面积，满足。

（Ⅰ）求角C的大小；

（Ⅱ）求的最大值。

 (Ⅰ)解：由题意可知

absinC=,2abcosC.

所以tanC=.

因为0<C<，

所以C=.

（Ⅱ)解：由已知sinA+sinB=sinA+sin(-C-A)=sinA+sin(-A)

                        =sinA+cosA+sinA=sin(A+)≤.

当△ABC为正三角形时取等号，

所以sinA+sinB的最大值是.

 [番茄花园1]1.

△ABC的内角A、B、C的对边分别为a、b、c，已知cos（A-C）＋cosB=1，a=2c，求c

【解析】解：因为

在△ABC中,内角A,B,C的对边分别为a,b,c.已知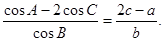

(1)求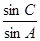的值;

(2)若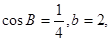求△ABC的面积S.

【解析】第一问中，利用

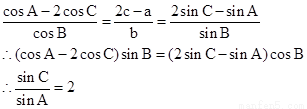
得到结论第二问中，因为即c=2a，然后利用余弦定理

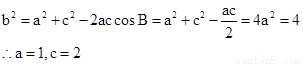
结合面积公式得到。

(1) 解：因为

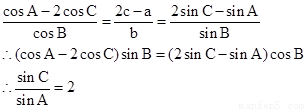
即

(2)因为即c=2a，然后利用余弦定理

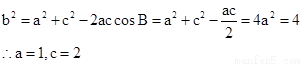
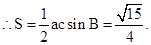
设不等边三角形ABC的外心与重心分别为M、G，若A（－1，0），B（1，0）且MG//AB.

（Ⅰ）求三角形ABC顶点C的轨迹方程；

（Ⅱ）设顶点C的轨迹为D，已知直线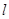过点（0，1）并且与曲线D交于P、N两点，若O为坐标原点，满足OP⊥ON，求直线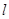的方程.

【解析】

第一问因为设C（x,y）（）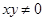

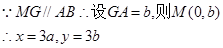……3分

∵M是不等边三解形ABC的外心，∴|MA|=|MC|，即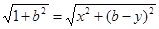（2）

由（1）（2）得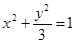.所以三角形顶点C的轨迹方程为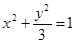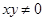，.…6分

第二问直线l的方程为y=kx+1

由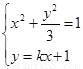消y得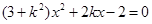。 ∵直线l与曲线D交于P、N两点，∴△=，

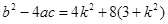又，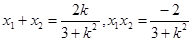

∵，∴

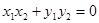
得到直线方程。