已知函数＝＋有如下性质：如果常数＞0，那么该函数在0，上是减函数，在，＋∞上是增函数．

（1）如果函数＝＋（＞0）的值域为6，＋∞，求的值；

（2）研究函数＝＋（常数＞0）在定义域内的单调性，并说明理由；

（3）对函数＝＋和＝＋（常数＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数＝＋（是正整数）在区间[，2]上的最大值和最小值（可利用你的研究结论）．

22．已知函数＝＋有如下性质：如果常数＞0，那么该函数在0，上是减函数，

在，＋∞上是增函数．

（1）如果函数＝＋（＞0）的值域为6，＋∞，求的值；

（2）研究函数＝＋（常数＞0）在定义域内的单调性，并说明理由；

（3）对函数＝＋和＝＋（常数＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数

＝＋（是正整数）在区间[，2]上的最大值和最小值（可利用你的研究结论）．

已知函数f(x)是定义在R上的函数，如果函数f(x)在R上的导函数f′(x)的图象如图，则有以下几个命题：

(1)f(x)的单调递减区间是(－2,0)、(2，＋∞)，f(x)的单调递增区间是(－∞，－2)、(0,2)；
(2)f(x)只在x＝－2处取得极大值；
(3)f(x)在x＝－2与x＝2处取得极大值；
(4)f(x)在x＝0处取得极小值．
其中正确命题的个数为                                                               (　　)

已知函数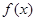的图像与函数h(x)＝x＋＋2的图像关于点A(0,1)对称．

(1) 求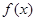的解析式；

(2) 若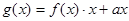，且g(x)在区间[0,2]上为减函数，求实数a的取值范围．

已知函数f(x)是定义在R上的函数，如果函数f(x)在R上的导函数f′(x)的图象如图，则有以下几个命题：

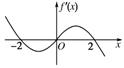
(1)f(x)的单调递减区间是(－2,0)、(2，＋∞)，f(x)的单调递增区间是(－∞，－2)、(0,2)；

(2)f(x)只在x＝－2处取得极大值；

(3)f(x)在x＝－2与x＝2处取得极大值；

(4)f(x)在x＝0处取得极小值．

其中正确命题的个数为                                                               (　　)

A．1                                               B．2

C．3                                               D．4