
题目列表(包括答案和解析)
用二分法求方程f(x)=0近似解中的算法共分以下5步,其中正确的顺序为
①确定有解区间[a,b](f(a)·f(b)<0).
②计算函数f(x)在中点处的函数值.
③判断新的有解区间的长度是否小于精确度:
a.如果新的有解区间的长度大于精确度,则在新的有解区间上重复上述步骤;
b.如果新的有解区间的长度小于或等于精确度,则取新的有解区间的中点为方程的近似解.
④取区间[a,b]的中点x=![]()
⑤判断函数值f![]() 是否为0:
是否为0:
a.如果为0,x=![]() 就是方程的解,问题得到解决;
就是方程的解,问题得到解决;
b.若f![]() 不为0,分两种情况:
不为0,分两种情况:
若f(a)·f![]() >0,确定新的有解区间为(
>0,确定新的有解区间为(![]() ,b).
,b).
①④②⑤③
①②③④⑤
①⑤②③④
①④⑤③②

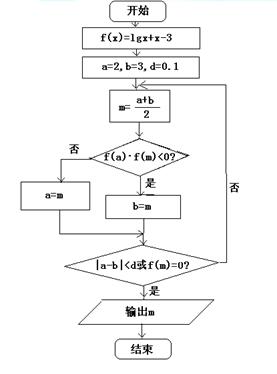
 如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为 如图是用二分法求方程lg x=3-x的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为
|
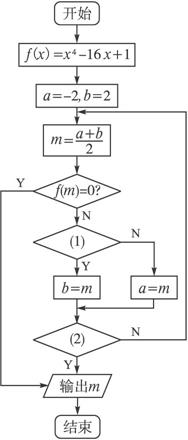
如图是用二分法求方程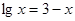 的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为( )
的近似解(精确度为0.1)的程序框图,则阅读程序框图并根据下表信息求出第一次满足条件的近似解为( )
|
根所在区间 |
区间端点函数值符号 |
中点值 |
中点函数值符号 |
|
(2,3) |
f(2)<0, f(3)>0 |
2.5 |
f(2.5)<0 |
|
(2.5,3) |
f(2.5)<0,f(3)>0 |
2.75 |
f(2.75)>0 |
|
(2.5,2.75) |
f(2.5)<0,f(2.75)>0 |
2.625 |
f(2.625)>0 |
|
(2.5,2.625) |
f(2.5)<0,f(2.625)>0 |
2.5625 |
f(2.5625)<0 |
|
(2.5625,2.625) |
f(2.5625)<0,f(2.625)>0 |
2.59375 |
f(2.59375)>0 |
|
(2.5625,2.59375) |
f(2.5625)<0,f(2.59375)>0 |
2.578125 |
f(2.578125)<0 |
|
(2.578125,2.59375) |
f(2.578125)<0,f(2.59375)>0 |
|
|
A.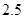 B.
B.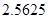
C.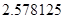 D.
D.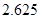
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com