
题目列表(包括答案和解析)
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(文)某种型号汽车的四个轮胎半径相同,均为 ,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑
,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑 形成顶角为
形成顶角为 的等腰三角形,且
的等腰三角形,且 ,如果地面上有
,如果地面上有 (
( )高的积水(此时坑内全是水,其它因素忽略不计).
)高的积水(此时坑内全是水,其它因素忽略不计).
(1)当轮胎与 、
、 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为 ;
;
(2) 假定该汽车能顺利通过这个坑(指汽车在过此坑时,符合涉水安全要求),求 的最大值.
的最大值.
(精确到1cm).
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为 ,公差为
,公差为 的无穷等差数列
的无穷等差数列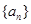 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项 ,第三项
,第三项 和第五项
和第五项 .
.
(1) 若 成等比数列,求
成等比数列,求 的值;
的值;
(2) 在 ,
,  的无穷等差数列
的无穷等差数列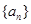 中,是否存在无穷子数列
中,是否存在无穷子数列 ,使得数列
,使得数列 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数 ,公比为正整数
,公比为正整数 (
( )的无穷等比数 列
)的无穷等比数 列 ,总可以找到一个子数列
,总可以找到一个子数列 ,使得
,使得 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列 中任取三项
中任取三项 ,由
,由 与
与 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
| (老教材) 设a为实数,方程2x2-8x+a+1=0的一个虚根的模是
(1)求a的值; (2)在复数范围内求方程的解. |
(新教材) 设函数f(x)=2x+p,(p为常数且p∈R) (1)若f(3)=5,求f(x)的解析式; (2)在满足(1)的条件下,解方程:f-1(x)=2+log2x2. |
(本题满分8分)求下列曲线的的标准方程:
(1) 离心率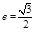 且椭圆经过
且椭圆经过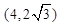 .
.
(2) 渐近线方程是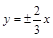 ,经过点
,经过点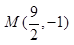 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com