
题目列表(包括答案和解析)
(本小题满分14分)
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M ,
AN⊥PC于N.
(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN.
(3)若PA=AB=4,设∠BPC=![]() ,试用
,试用![]() 表示△AMN 的面积,当
表示△AMN 的面积,当![]() 取何值时,
取何值时,
△AMN的面积最大?最大面积是多少?

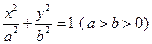 的两个焦点为
的两个焦点为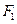 、
、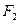 ,短轴两个端点为
,短轴两个端点为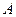 、
、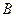 .已知
.已知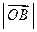 、
、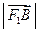 、
、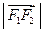 成等比数列,
成等比数列,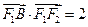 ,与
,与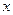 轴不垂直的直线
轴不垂直的直线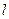 与C 交于不同的两点
与C 交于不同的两点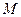 、
、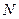 ,记直线
,记直线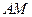 、
、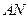 的斜率分别为
的斜率分别为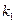 、
、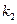 ,且
,且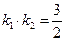 .
.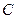 的方程;
的方程;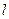 与
与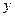 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;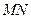 的中点
的中点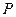 落在四边形
落在四边形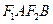 内(包括边界)时,求直线
内(包括边界)时,求直线 的斜率的取值范围.
的斜率的取值范围.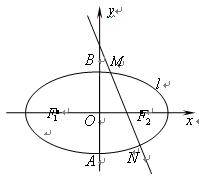
(本小题满分14分)
设函数 ,其中
,其中 .
.
( I )若函数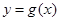 图象恒过定点P,且点P在
图象恒过定点P,且点P在 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当 时,设
时,设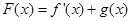 ,讨论
,讨论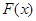 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设 ,曲线
,曲线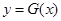 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
(本小题满分14分)
设函数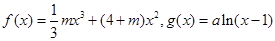 ,其中
,其中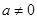 .
.
( I )若函数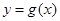 图象恒过定点P,且点P在
图象恒过定点P,且点P在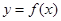 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当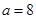 时,设
时,设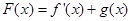 ,讨论
,讨论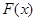 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设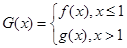 ,曲线
,曲线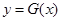 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
如图,在直角三角形ABC中,AD是斜边BC上的高,有很多大家熟悉的性质,例如“AB⊥AC”,勾股定理“|AB|2+|AC|2=|BC|2”和“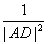 =
=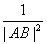 +
+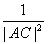 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
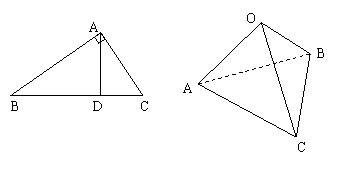 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com