
题目列表(包括答案和解析)
已知平面向量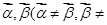 0)满足
0)满足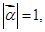
(1)当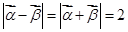 时,求
时,求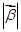 的值;
的值;
(2)当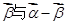 的夹角为
的夹角为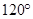 时,求
时,求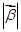 的取值范围。
的取值范围。
、已知直线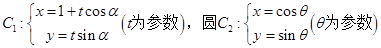 .
.
(1) 当 时,求
时,求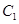 与
与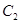 的交点;
的交点;
(2)设曲线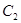 经过伸缩变换
经过伸缩变换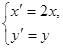 得到曲线
得到曲线 ,设曲线
,设曲线 上任一点为
上任一点为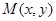 ,
,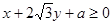 恒成立,求
恒成立,求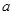 的取值范围。
的取值范围。
已知函数
(1)当 时,求
时,求 上的最大值、最小值:
上的最大值、最小值:
(2)求 的单调区间;
的单调区间;
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为![]() ,出现“×”的概率为
,出现“×”的概率为![]() .若第
.若第![]() 次出现“○”,则a
次出现“○”,则a![]() =1;出现“×”,则a
=1;出现“×”,则a![]() =
=![]() .令S
.令S![]() =a
=a![]() +a
+a![]() +…+a
+…+a![]()
![]() .
. ![]() 学科网
学科网
(1)当![]() 时,求S
时,求S![]()
![]() 2的概率;
2的概率;
(2)当![]()
![]() ,
,![]()
![]() 时,求S
时,求S![]() =2且S
=2且S![]() ≥0(i=1,2,3,4)的概率.
≥0(i=1,2,3,4)的概率.
已知

(1)当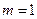 时,求
时,求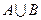 ;
;
(2) 若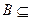
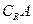 ,求实数
,求实数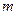 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com