已知函数f(x)＝，其中a，b满足a·b≠0.

(1)若a·b>0，判断函数f(x)的单调性；

(2)若a·b<0，求f(x＋1)>f(x)时的x的取值范围．

已知函数f(x)＝ax²＋1(a>0)，g(x)＝x³＋bx.

(1)若曲线y＝f(x)与曲线y＝g(x)在它们的交点(1，c)处具有公共切线，求a，b的值；

(2)当a²＝4b时，求函数f(x)＋g(x)的单调区间，并求其在区间(－∞，－1]上的最大值．

已知函数f(x)＝－x³－ax²＋b²x＋1(a、b∈R)．

(1)若a＝1，b＝1，求f(x)的极值和单调区间；

(2)已知x₁，x₂为f(x)的极值点，且|f(x₁)－f(x₂)|＝|x₁－x₂|，若当x∈[－1,1]时，函数y＝f(x)的图象上任意一点的切线斜率恒小于m，求m的取值范围

已知函数f(x)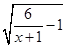＝的定义域为集合A，函数g(x)＝lg(－x²＋2x＋m)的定义域为集合B.
(1)当m＝3时，求A∩(∁_RB)；
(2)若A∩B＝{x|－1＜x＜4}，求实数m的值．

已知函数f(x)＝|ax－2|＋bln x(x>0，实数a，b为常数)．
(1)若a＝1，f(x)在(0，＋∞)上是单调增函数，求b的取值范围；
(2)若a≥2，b＝1，求方程f(x)＝在(0,1]上解的个数．