（本小题满分12分）

椭圆G:的左、右焦点分别为，M是椭圆上的一点,且满足=0．

   （1）求离心率e的取值范围；

   （1）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为5．

①求此时椭圆G的方程；

②设斜率为的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，

问：A、B两点能否关于过点、Q的直线对称？若能，求出k的取值范

围；若不能，请说明理由．

（本小题满分12分）2010年广东亚运会，某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作，比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的，根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：

甲系列：

乙系列：

 现该运动员最后一个出场，其之前运动员的最高得分为118分。

（I）                    若该运动员希望获得该项目的第一名，应选择哪个系列，说明理由，并求其获得第一名的概率；

（II）                 （II）若该运动员选择乙系列，求其成绩X的分布列及其数学期望EX。

（本小题满分12分）

        已知实轴长为2a，虚轴长为2b的双曲线S的焦点在x轴上，直线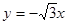是双曲线S的一条渐近线，而且原点O，点A（a，0）和点B（0，-b）使等式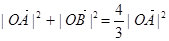·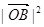成立.

   （I）求双曲线S的方程；

   （II）若双曲线S上存在两个点关于直线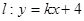对称，求实数k的取值范围.

（本小题满分12分）设函数.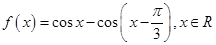

（1）求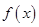的最大值，并求取得最大值时x的取值集合；

（2）记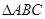的内角A、B、C的对边分别为a，b，c，若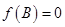，b=1，c=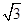，求a的值.[来源:Z+xx+k.Com]

（本小题满分12分）

已知当k得值是多少时？

直线平行