
题目列表(包括答案和解析)
(本小题满分8分)
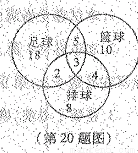
一个学校的足球队、篮球队和排球队分别有28,22,17名成员,一些成员不止参加一支球队,具体情况如图所示,随机选取的一名成员:
(1) 属于不止1支球队的概率是多少?
(2) 属于不超过2支球队的概率是多少?
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
|
尺寸 |
|
|
|
|
|
|
|
甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
|
乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y( 码 ) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序 号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y( 码 ) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的![]() 联列表:
联列表:
| 高 个 | 非高个 | 合 计 | |
| 大 脚 | |||
| 非大脚 | 12 | ||
| 合 计 | 20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):

 男 女
男 女
 15
7 7 8 9 9 9
15
7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
(本小题满分13分)经过市场调查发现,某种产品投放市场的100天中,前40天其价格直线上升,而后60天其价格则呈直线下降趋势.现抽取其中4天的价格如下表所示:
| 时间(天) | 第8天 | 第32天 | 第70天 | 第90天 |
| 价格(千元) | 24 | 30 | 17 | 7 |
⑴写出投放市场的第![]() 天的价格关于时间
天的价格关于时间![]() 的函数表达式.
的函数表达式.
⑵若销售量![]() 与时间
与时间![]() (天)的函数关系式是
(天)的函数关系式是![]() (1≤x≤100且
(1≤x≤100且![]() )问该产品投放市场第几天时,日销售额最大,最大值是多少?
)问该产品投放市场第几天时,日销售额最大,最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com