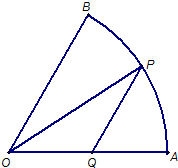已知扇形OAB的半径为3，圆心角∠AOB=60°，过弧AB上的动点P作平行于BO的直线交AO于点Q，设∠AOP=θ．
（1）求△POQ的面积S关于θ的函数解析式S=f（θ）；
（2）θ为何值时，S=f（θ）有最大值？并求出该最大值．

国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动．为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如表所示：

序号（i）	每天睡眠时间 （小时）	组中值 （mi）	频数	频率 （fi）
1	[4，5）	4.5	8	0.10
2	[5，6）	5.5	52	0.20
3	[6，7）	6.5	60	0.30
4	[7，8）	7.5	56	0.25
5	[8，9）	8.5	20	0.10
6	[9，10）	9.5	4	0.05

（1）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；
（2）该网站利用如图所示的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义．

为普及高中生安全逃生知识与安全防护能力，某学校高一年级举办了高中生安全知识与安全逃生能力竞赛．该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛．先将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．

分数（分数段）	频数（人数）	频率
[60，70）	9	x
[70，80）	y	0.38
[80，90）	16	0.32
[90，100）	z	s
合   计	p	1

（Ⅰ）求出上表中的x，y，z，s，p的值；
（Ⅱ）按规定，预赛成绩不低于90分的选手参加决赛，参加决赛的选手按照抽签方式决定出场顺序．已知高一•二班有甲、乙两名同学取得决赛资格．
①求决赛出场的顺序中，甲不在第一位、乙不在最后一位的概率；
②记高一•二班在决赛中进入前三名的人数为X，求X的分布列和数学期望．