
题目列表(包括答案和解析)
(本小题满分16分)
对于函数y=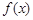 ,x∈(0,
,x∈(0,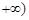 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么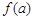 ,
,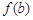 ,
,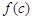 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数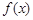 为“保三角形函数”.
为“保三角形函数”.
对于函数y=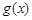 ,x∈
,x∈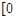 ,
,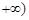 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有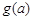 ,
,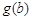 ,
,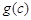 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数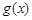 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“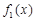 =x,
=x,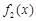 =
=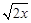 ,
,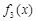 =
=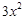 (定义域均为x∈(0,
(定义域均为x∈(0,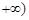 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数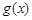 =
=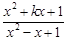 ,x∈
,x∈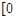 ,
,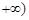 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数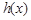 是定义在(0,
是定义在(0,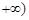 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,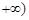 ,试证明:
,试证明: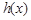 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
(本小题满分14分)
市政府为招商引资,决定对外资企业第一年产品免税.某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件.第二年,当地政府开始对该商品征收税率为p%(0<p<100,即销售100元要征收p元)的税收,于是该产品的出厂价上升为每件 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(Ⅰ)将第二年政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(Ⅱ)要使第二年该厂的税收不少于16万元,则税率p%的范围是多少?
(Ⅲ)在第二年该厂的税收不少于16万元的前提下,要让厂家获得最大销售金额,则p
应为多少?
(本小题满分16分)
对于函数y=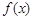 ,x∈(0,
,x∈(0,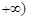 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么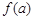 ,
,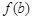 ,
,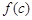 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数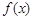 为“保三角形函数”.
为“保三角形函数”.
对于函数y=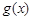 ,x∈
,x∈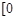 ,
,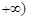 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有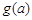 ,
,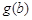 ,
,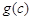 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数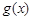 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“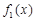 =x,
=x,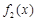 =
=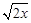 ,
,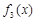 =
=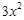 (定义域均为x∈(0,
(定义域均为x∈(0,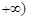 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数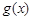 =
=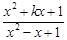 ,x∈
,x∈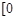 ,
,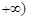 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数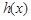 是定义在(0,
是定义在(0,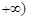 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,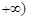 ,试证明:
,试证明: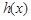 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
(本小题满分16分:8+8)
给出函数封闭的定义:若对于定义域D内的任一个自变量 ,都有函数值
,都有函数值 ,则称函数y=f(x)在 D上封闭。
,则称函数y=f(x)在 D上封闭。
(1)若定义域 判断下列函数中哪些在
判断下列函数中哪些在 上封闭,并给出推理过程;
上封闭,并给出推理过程;

(2)若定义域 是否存在实数
是否存在实数 ,使函数
,使函数 在
在 上封闭,若存在,求出
上封闭,若存在,求出 值,若不存在,请说明理由。
值,若不存在,请说明理由。
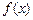 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么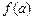 ,
,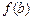 ,
,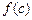 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数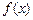 为“保三角形函数”.
为“保三角形函数”. ,x∈
,x∈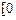 ,
, ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有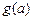 ,
,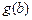 ,
,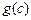 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数 为“恒三角形函数”.
为“恒三角形函数”.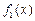 =x,
=x, =
=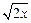 ,
,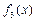 =
=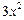 (定义域均为x∈(0,
(定义域均为x∈(0, )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由; =
=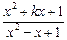 ,x∈
,x∈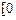 ,
, 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围; 是定义在(0,
是定义在(0, 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0, ,试证明:
,试证明: 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com