
题目列表(包括答案和解析)
(本小题满分14分)
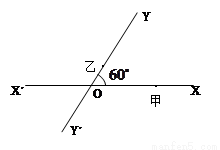
如图,有两条相交成 的直路
的直路 ,
,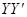 ,交点是
,交点是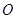 ,甲、乙分别在
,甲、乙分别在 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿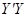 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在 上点A处,乙在
上点A处,乙在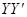 上点B处.
上点B处.
(Ⅰ)求t=1.5时,甲、乙两人之间的距离;
(Ⅱ)求t=2时,甲、乙两人之间的距离;
(Ⅲ) 当t为何值时,甲、乙两人之间的距离最短?
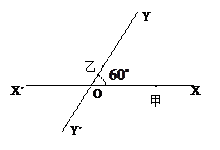
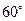 的直路
的直路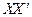 ,
,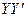 ,交点是
,交点是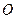 ,甲、乙分别在
,甲、乙分别在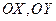 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿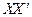 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿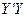 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在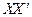 上点A处,乙在
上点A处,乙在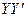 上点B处.
上点B处.(本小题满分14分)
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为![]() ,两镇的中心
,两镇的中心![]() 相距8个单位距离,环形高速公路所在的曲线为
相距8个单位距离,环形高速公路所在的曲线为![]() ,且
,且![]() 上的点到
上的点到![]() 的距离之和为10个单位距离,在曲线
的距离之和为10个单位距离,在曲线![]() 上建一个加油站
上建一个加油站![]() 与一个收费站
与一个收费站![]() ,使
,使![]() 三点在一条直线上,并且
三点在一条直线上,并且![]() 个单位距离.
个单位距离.
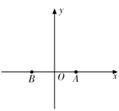 (1) 建立如图的直角坐标系,求曲线
(1) 建立如图的直角坐标系,求曲线![]() 的方程及
的方程及![]() 之间的距离有多少个单位距离;
之间的距离有多少个单位距离;
(2) ![]() 之间有一条笔直公路
之间有一条笔直公路![]() 与X轴正方向成
与X轴正方向成![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,该县招商部门引进外资在四边形
两点,该县招商部门引进外资在四边形![]() 区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
(本小题满分14分) 已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数![]() 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数![]() 与
与![]() 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求![]() 的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作
的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作![]() 轴的垂线分别与
轴的垂线分别与![]() 的图像和
的图像和![]() 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作![]() 的切线
的切线![]() ,以T为切点作
,以T为切点作![]() 的切线
的切线![]() .是否存在实数
.是否存在实数![]() 使得
使得![]()
![]()
![]() ,如果存在,求出
,如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分14分) 已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数![]() 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数![]() 与
与![]() 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求![]() 的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作
的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作![]() 轴的垂线分别与
轴的垂线分别与![]() 的图像和
的图像和![]() 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作![]() 的切线
的切线![]() ,以T为切点作
,以T为切点作![]() 的切线
的切线![]() .是否存在实数
.是否存在实数![]() 使得
使得![]()
![]()
![]() ,如果存在,求出
,如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com