
题目列表(包括答案和解析)
(本题满分8分)如图,在底面是矩形的四棱锥
 中,
中, 底面
底面 ,
, 分
分
别是 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面 .高.考.资.源.网
.高.考.资.源.网
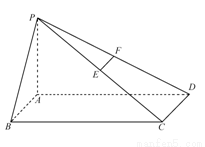
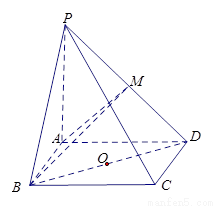
(理)(本小题8分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,
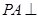 平面
平面 ,
,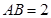 ,
, ,以
,以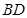 的中点
的中点 为球心、
为球心、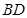 为直径的球面交
为直径的球面交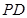 于点
于点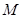 .
.
(1) 求证:平面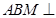 平面
平面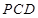 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
证明:(1)由题意,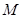 在以
在以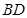 为直径的球面上,则
为直径的球面上,则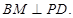
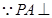 平面
平面 ,则
,则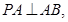
又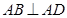 ,
,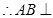 平面
平面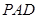 ,
,
∴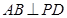 ,
,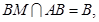
 平面
平面 ,
,
∴平面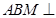 平面
平面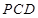 . (3分)
. (3分)
(2)∵ 是
是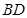 的中点,则
的中点,则 点到平面
点到平面 的距离等于点
的距离等于点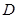 到平面
到平面 的距离的一半,由(1)知,
的距离的一半,由(1)知,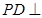 平面
平面 于
于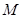 ,则线段
,则线段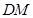 的长就是点
的长就是点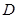 到平面
到平面 的距离
的距离

∵在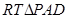 中,
中,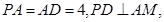
∴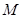 为
为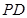 的中点,
的中点,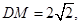 (7分)
(7分)
则点 到平面
到平面 的距离为
的距离为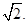 (8分)
(8分)
(其它方法可参照上述评分标准给分)
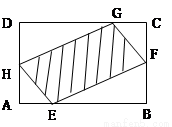
(本题满分8分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?
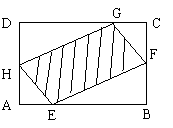
(本题满分8分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?
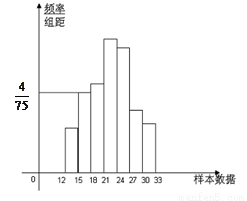
(本小题满分10分)如图是总体的一个样本频率分布直方图,且在[15,18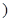 内频数为8.
内频数为8.
(1)求样本在[15,18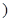 内的频率;
内的频率;
(2)求样本容量;
(3)若在[12,15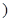 内的小矩形面积为0.06,求在[18,33
内的小矩形面积为0.06,求在[18,33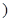 内的频数.
内的频数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com