
题目列表(包括答案和解析)
(本题满分16分)如图,已知点 是正方形
是正方形 所在平面外一点,
所在平面外一点,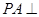 平面
平面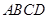 ,
,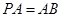 ,点
,点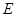 、
、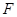 分别在线段
分别在线段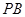 、
、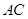 上,满足
上,满足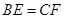 .
.
(1)求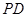 与平面
与平面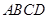 所成的角的大小;
所成的角的大小;
(2)求平面PBD与平面ABCD所成角的正切值。
(3)求证: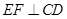 ;
;
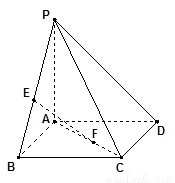
(本题满分16分)
如图,椭圆C: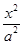 +
+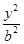 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
点(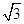 ,
,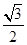 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.
(1) 求椭圆C的方程;
(2) 点P是椭圆C上的动点,PQ ⊥l,垂足为Q.
是否存在点P,使得△F1PQ为等腰三角形?
若存在,求出点P的坐标;若不存在,说明理由.
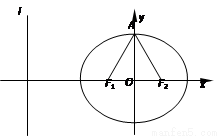
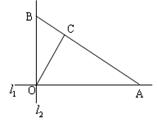
(本题16分)如图,在 城周边已有两条公路
城周边已有两条公路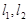 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为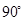 .已知
.已知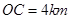 ,
, 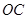 与公路
与公路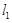 夹角为
夹角为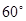 .现规划在公路
.现规划在公路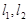 上分别选择
上分别选择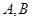 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过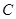 城.设
城.设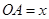
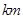 ,
,
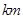 .
.
(1) 求出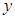 关于
关于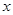 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域;
(2) 试确定点A,B的位置,使△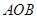 的面积最小.
的面积最小.
(本题16分)
如图所示,某人在斜坡P处仰视正对![]() 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为![]() ,
,![]()
(1)以射线OC为![]() 轴的正向,OB为
轴的正向,OB为![]() 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求![]() 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).

(本小题满分16分)
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com