
题目列表(包括答案和解析)
(本小题满分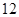 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
|
|
不及格 |
及格 |
总计 |
|
甲班 |
10 |
35 |
M |
|
乙班 |
7 |
38 |
45 |
|
总计 |
17 |
73 |
N |
(1) 求M,N的值
(2) 写出求k 观测值的计算式
观测值的计算式
(3) 假设k =0.6527你有多大把握认为成绩及格与班级有关?
=0.6527你有多大把握认为成绩及格与班级有关?
k =7.121又说明什么?
=7.121又说明什么?
(P(k
 )
)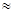 0.100,P(k
0.100,P(k
 )
)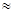 0.010)
0.010)
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
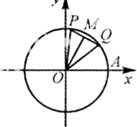
如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为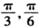 (单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中
(单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中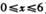 ),
),
(I)求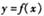 的函数解析式;
的函数解析式;
(II)将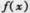 图象上的各点均向右平移2个单位长度,得到
图象上的各点均向右平移2个单位长度,得到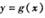 的图象,求函数
的图象,求函数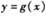 的单调递减区间.
的单调递减区间.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17. (本小题满分10分)
已知复数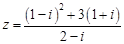 ,若
,若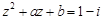 ,
,
⑴求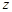 ;
;
⑵求实数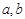 的值
的值
(17) (本小题满分10分)(注意:在试题卷上作答无效)
设等差数列{![]() }的前
}的前![]() 项和为
项和为![]() ,公比是正数的等比数列{
,公比是正数的等比数列{![]() }的前
}的前![]() 项和为
项和为![]() ,
,
已知![]() 的通项公式.
的通项公式.
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
|
尺寸 |
|
|
|
|
|
|
|
甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
|
乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com